Markov chain geostatistics

Go Back

The Small Class Underestimation Problem

Small class underestimation (or underrepresentation) herein means that the occurrence (percentage) of a small class in simulated realizations (proportion data should be averaged from a number of simulated realizations) is obviouslly less than its due proportion (e.g., its proprotion in sample data). This problem is also reflected on optimal maps based on maximum occurrence probabilities. If the proportions of a small class in different data sets (e.g., a dense data set and a sparse data set) are different, its simulated proportions should be different. If a small class happens to have a high proportion in a dense sample data set and a low proportion in a sparse sample data set, its low simulated proportion with the sparse sample data set should not be mistakenly regarded as an underestimation. In addition, input parameters (here transiogram models) also impact simulated proportions. Note that small classes herein mean those classes with area proportions less than the average, not simply the smallest or a very minor class.

Small class underestimation is an irrational feature observed in simulated results of the coupled Markov chain (CMC) model (Elfeki 1996; Elfeki and Dekking 2001) and its extensions (e.g., the triplex Markov chain model) (Li et al. 2004). In unconditional simulations (conditioned only on top and left boundaries), small classes can be strongly underestimated and minor classes usually disappear in simulated realizations of the CMC model; this situation is especially apparent for horizontal soil type pattern simulation (see Li 1999 postdoc report). In conditional simulations (conditioned on boreholes, survey lines, or scattered sample data), the degrees of underestimation of small classes depend on the densities of observed data (see Li et al. 2004; Zhang and Li 2008). The problem was specifically discussed and analyzed with class proportion data in simulated realizations in Li et al. (2004). This small-class underestimation problem was finally solved by the Markov chain random field (MCRF) theory and models (see Li 2007).

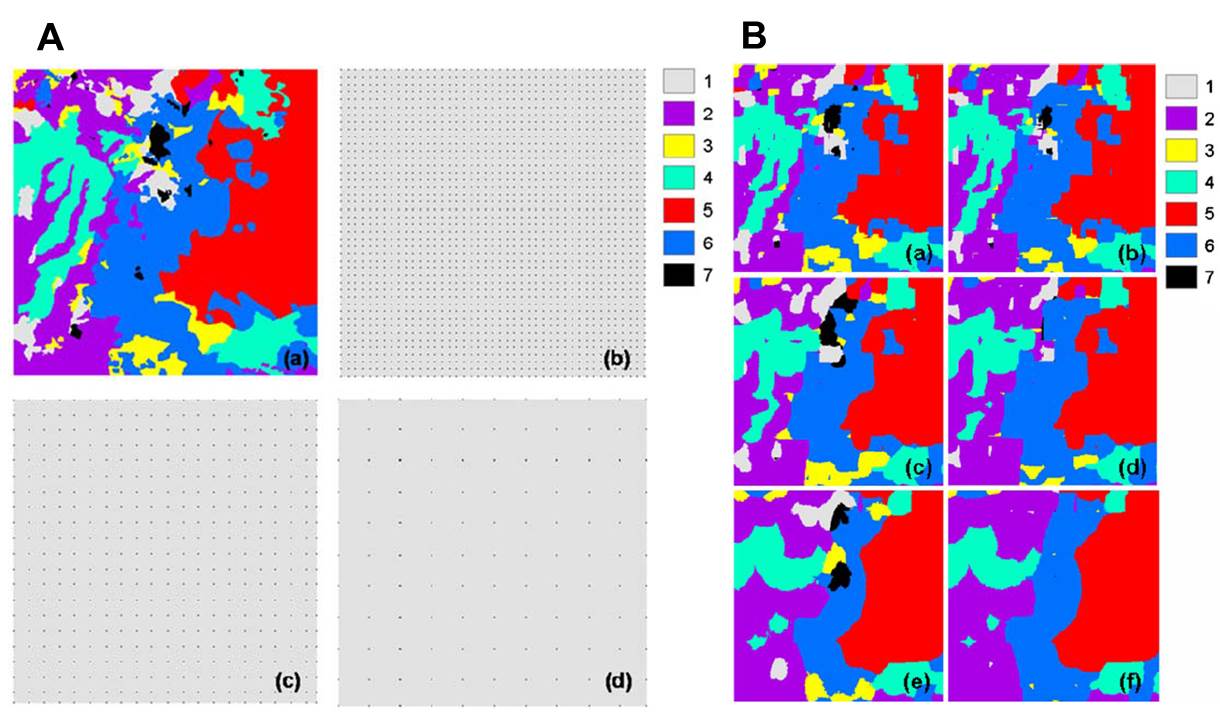
Because borehole data and survey line data are continuous line data, they have better effect in reducing the small class underestimation trend. However, for scattered point sample data, a very high density may be necessary to effectively overcome the small class underestimation problem of the CMC model and its extensions. When the density of sample data is relatively low, minor classes are usually gone. In addition, with decreasing density of samples, the simulated pattern becomes simpler, and finally only a few polygons of large classes are left (see Figure 1, which shows simulated optimal maps based on maximum occurrence probabilities using a simplified MCRF model and the CMC-based triplex Markov chain model).

Figure 1. Comparison of simulated optimal maps using the CMC-based triplex Markov chain model and a simplified MCRF model (from Zhang and Li 2008). A: Original categorical map (295 × 295 pixels) (a) and three regular sample data sets (b -1849, c - 441, and d - 121 data). B: Left column - simulated optimal maps using the simplified MCRF model, which do not have the small class underestimation problem, based on the dense (a), medium (c) and sparse (e) sample data sets. Right column – simulated optimal maps using the CMC-based triplex Markov chain model, which show apparent small class underestimation, based on the dense (b), medium (d) and sparse (f) sample data sets.

Although they misunderstood Markov chain modeling and our studies (and the new avenues they suggested were statistically wrong even if they imitated the MCRF model), Cao and Kyriakidis (2008) made an unconditional simulation (without any sample data) using the CMC-based triplex Markov chain (TMC) model and their result demonstrated the small-class underestimation problem (see Figure 2), which, as a major issue, had been analyzed and discussed in Li et al. (2004). However, they did not mention the work of Elfeki and Dekking (2001), and only cited our earlier work that aimed to improve and extend the CMC model. We had been making large effort to solve the problem and actually had solved it with the Markov chain random field (MCRF) model and published the MCRF solution in 2007 (Li 2007). Unfortunately, they mixed the concepts in the series of studies of ours together, and consequently made some confusing and irrational statements, such as "We would like to end this paper with a warning against the uninformed use of SMC under conditional independence: ......". In fact, there is no conditional independence assumption used in the CMC model or the CMC-based triplex Markov chain model, and we also did not use the term "spatial Markov chain" in our earlier papers for modifying the CMC model. The correct idea to solve the small class underestimation problem of the CMC model is the MCRF idea (which used the term "spatial Markov chain" and the conditional independence assumption for spatial data), which was suggested by Li in manuscripts in 2004 although its final publication had to be delayed to 2007 (see Li 2007). In recent years since 2007, the conditional independence assumption for nearest data within a neighborhood, which was initially extended by Li from a property of Pickard random fields, had been used by many researchers in spatial statistics and computation, no matter whether they respected our contribution or not.

Figure 2. A simulated realization using the CMC-based triplex Markov chain (TMC) model without sample data (adapted from Cao and Kyriakidis 2008). (a) Original map (generated by truncated Gaussian simulation) with three classes (proportions: 0.35, 0.4 and 0.25). (b) Simulated realization map. The TMC model effectively eliminated the parcel inclination problem of the previous CMC model, but could not eliminate the small-class underestimation problem, which reaches the extreme when no sample data are available.

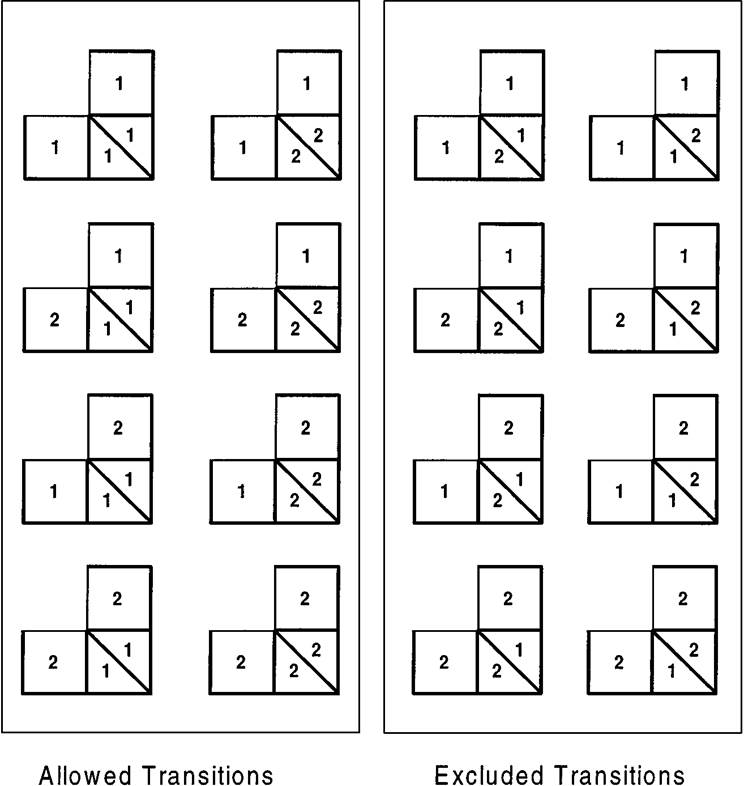
The CMC model sounded quite reasonable. So we were surprised by the small class underestimation problem appearing in our simulated results using the CMC model. At the beginning, we did not know what caused the small class underestimation problem and even attributed it to other reasons such as parameter estimation errors. Later, we gradually realized that the problem should be caused by the exclusion of conflict transitions (i.e., unwanted transitions), because this is the main theoretical defect of the CMC model. Elfeki and Dekking (2001) described the exclusion of conflict transitions for a two-class case in a figure (see Figure 4): When there are two classes, half transitions are conflict and have to be excluded in the CMC model so that simulation can be performed. Apparently, with increasing number of classes, more transitions will be conflict and have to be excluded (similarly, when more than two 1D Markov chains are multiplied together, there will also be more conflict transitions to be excluded). Unfortunately, they did not explore the possible consequence of such a treatment (i.e., assuming that two Markov chains only move to a location with equal states). Without data analysis of simulated realizations with varying lateral extensions among different geological layer types, despite the fact that they observed “geological features with short extensions were not very well reproduced” (Elfeki and Dekking 2001, p. 586; also see Figure 5 and Figure 6), it seemed that they did not find the general trend of small class underestimation in simulated results. My later guess that exclusion of conflict transitions causes small class underestimation was finally theoretically proven in Li (2007, p. 324).

Figure 4. Exclusion of conflict transitions in the coupled Markov chain model (from Elfeki and Dekking 2001)

Figure 5. Simulated 2D subsurface vertical sections using the coupled Markov chain model (from Elfeki and Dekking 2001, figure 6). Second row shows borhole data for conditioning. Third row shows simulated realizations using the conditional CMC model and fourth row shows simulated realizations using the uncodnitional CMC model. Note that this figure is the figure 6 in Elfeki and Dekking (2001). It is clear that small classes were strongly underestimated in simulated realizations when conditioning borehole data were not dense enough for the conditional CMC model, although the layer inclination problem was not apparent because the layers were extremely thin and straight. The unconditional CMC model could not work well in this simulation even when boreholes are dense, because the layer inclination tendency and the small class underestimation tendency together made the simulated thin layers end quickly. Small class underestimation is not only related with class proportions but also with class authocorelation strengths (i.e., magnitudes of self-transition probabilities). That is why long-straight layer types (whose self-transition probabilities are close to 1.0) were generated much better than short-straight layer types. Please note that in this figure, the major layer class is the class 8 in white color, which was overestimated in simulated realizations.

Figure 6. Simulated 2D subsurface vertical sections using the coupled Markov chain model (from Elfeki and Dekking 2001, figure 8). It is clear that small classes were strongly underestimated in simulated realizations when conditioning borehole data were not dense enough for the conditional CMC model, although the layer inclination problem was not apparent because the layers were extremely thin and straight. Small class underestimation is not only related with class proportions but also with class authocorelation strengths (i.e., magnitudes of self-transition probabilities). That is why long-straight layer types (whose self-transition probabilities in lateral direction are close to 1.0) were generated much better than short-straight layer types.

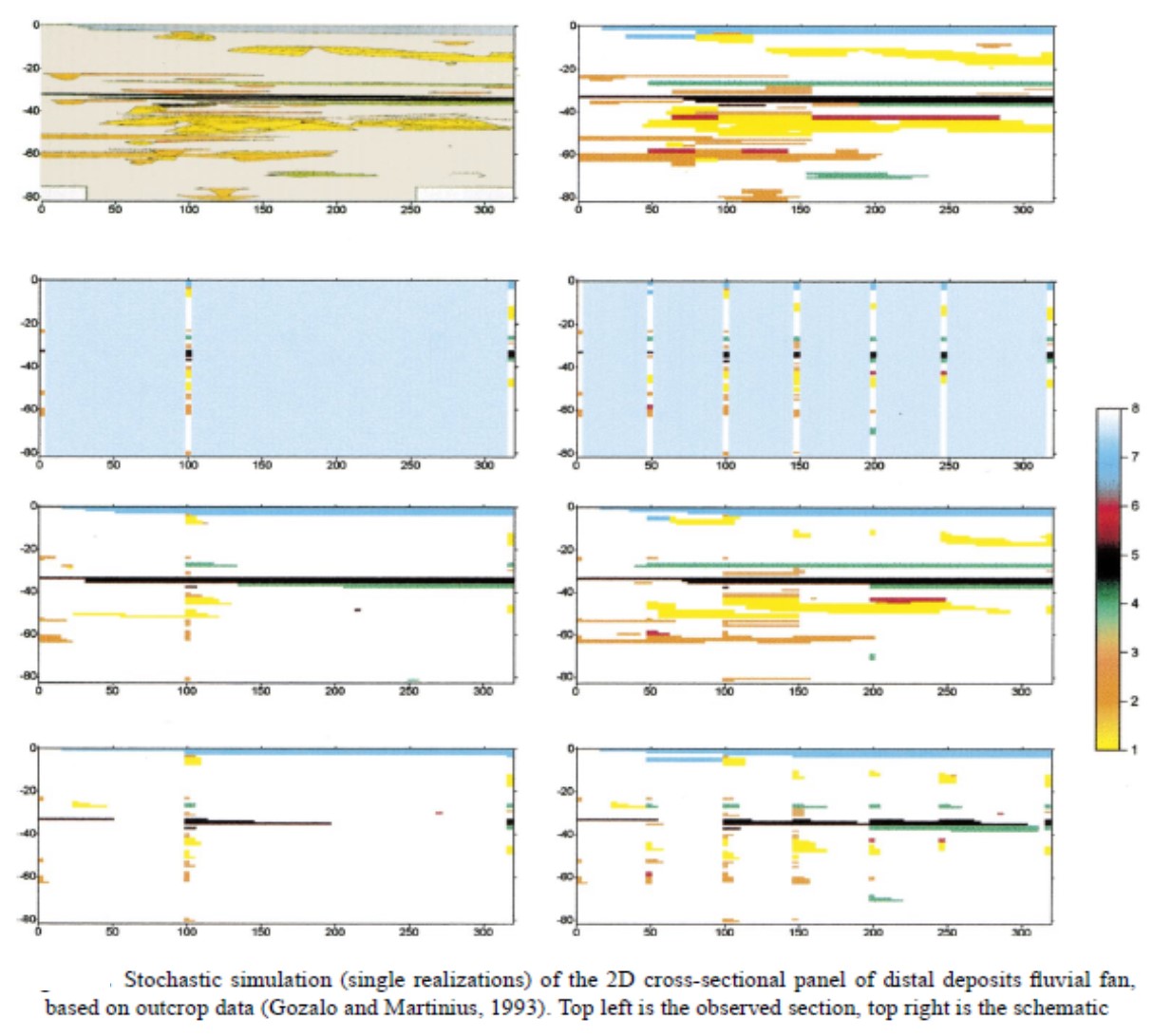
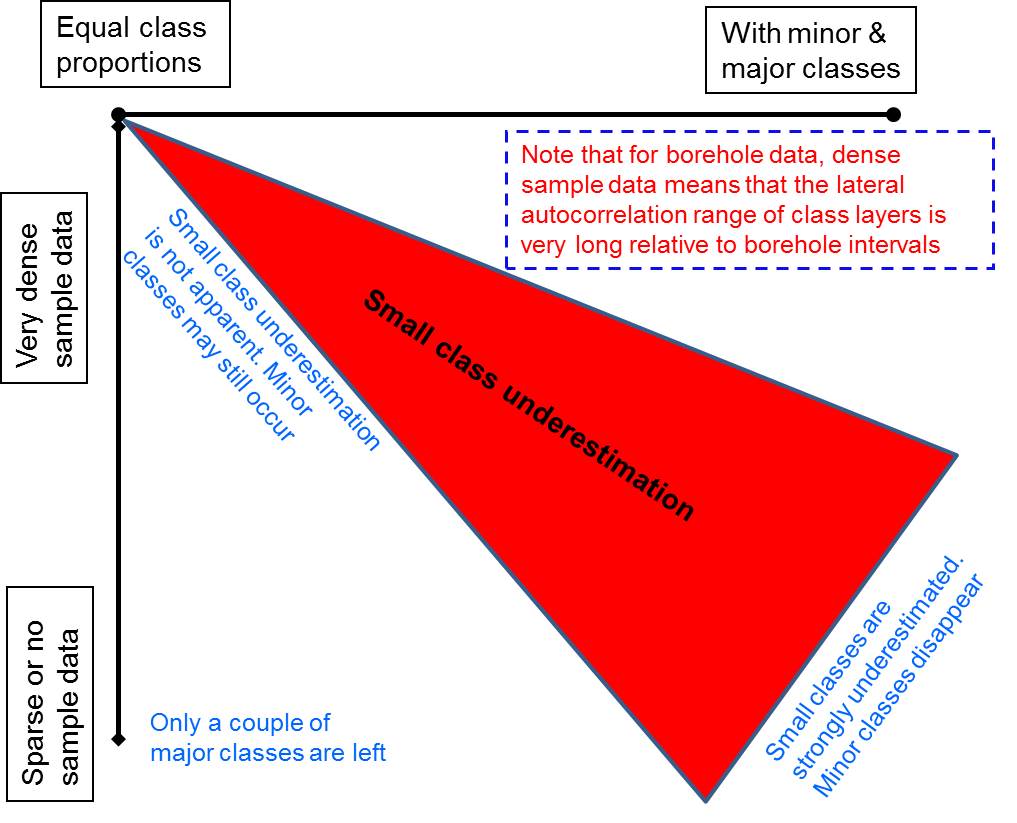
About the small class underestimation problem, there apparently exists a misunderstanding. For example, the misleading paper of Huang et al. (2016, IJGIS, p. 1442) stated "Li (2007b) showed that when large differences exist in the proportion of various classes, such as 10% for class 1 and 90% for class 2, using coupled Markov chain (CMC) idea of Elfeki and Dekking (2001) in calculating the conditional probability distribution of a random variable will get the occurrence probability of class 1, the small class, at about 1.2% and that of class 2, the large class, at about 98.8%. While the MCRF method, as a type of MCP, can solve this problem. Our analysis indicates that this statement is appropriate only when the class proportions have significant differences. When the proportion of various types is almost equal to each other, such as 25% or so for each class with four lithology types, the calibrated BBU approach is preferred". This understanding is not only wrong but also misleading. The simple example in Li (2007, p. 324) for proving the small class underestimation problem of the CMC model only gave the calculated probabilities for estimating the current grid cell (i.e., the CMC moves forward one cell). No spatial simulation only simulates one grid cell in a simulation case or a real application. With the simulation continuing forward, the small class underestimation problem will quickly propagate exponentially and the small class (even if it is a little smaller) will soon disappear in unconditional simulation, as shown in above Figure 2. In conditional simulation, unless there are dense point sample data to adjust the simulation, the small class underestimation problem will be very clear, as shown in above Figure 1. Using line sample data has better effect in reducing the problem, but the problem is still clear in simulating subsurface layers with borehole data, as shown in above Figures 5 and 6. Of course, when different classes or layer types have similar proportions, the problem is not clear, especially in conditional simulation. However, those cases that have all classes with similar proportions are obviously rare in the reality. Here the problem is mathematical, and we were talking about the normal cases. Arguing on the plausible results of the rare special cases (e.g. equal class proportions, naturally inclined patterns along the simulation direction, straight long layers) generated by the CMC model is meaningless, misleading, and also dishonest. In addition, the so-called MCP (Markovian-type categorical prediction) method was just an irrational insult to Li (2007) by tricks. The following Figure 7 explains the question - under what situations the small class underestimation problem occurs with different degrees.

Figure 7. The situations under which the small class underestimation problem of the CMC model occurs with different degrees. Note that the small class underestimation tendency always exists even if there are extremely dense sample data and the underestimation is not clear, because it is a theoretical problem.

Efforts to solve the small class underestimation problem

Attempt one: Our first attempt to cope with the small class underestimation problem was conducted within the framework of the CMC model. The idea was purely empirical and finally proved to be impractical. Considering that increasing conditioning data may reduce the small class underestimation effect, my idea was to “use artificial survey data”, that is, to insert simulated lines. One-dimensional Markov chains do not underestimate small classes. So we used 1-D Markov chain models to simulate a number of simulated lines and inserted them as conditioning data into the simulation grid of a vertical soil layer section being simulated. Although it is empirical, this idea indeed has good effect. Here is the manuscript we wrote in 2003 and revised in 2004, which described and tested the idea. This manuscript was submitted to a journal in water resource research and was reviewed. A resubmission with revisions was suggested by the editor in Spring 2004. I revised it, but never resubmitted it for publication, although it might be accepted for publication if resubmitted. The reasons were complex, but the major one was the imperfection of the idea – the inserted simulated lines are not correlated with each other because they were generated by 1D Markov chain models. This drawback was pointed out by one reviewer. So I wanted to first solve the correlation problem and then see whether the idea was still effective or not. After I developed computer programs to make the inserted simulated lines fully correlated with each other, I found that the inserted simulated lines had no effect anymore -- Because I had to use an extended CMC model to generate the simulated lines so that they were correlated each other, small classes were also underestimated in the inserted simulated lines. This meant that the attempt failed theoretically. Publishing a valueless paper with page charge was apparently unreasonable, especially when a research had no funding support. So I finally discarded the manuscript.

Attempt two: With increasing understandings on the issue, our second attempt to solve the problem was to implement the “single chain” idea (see Li 2007), which finally resulted in the Markov chain random field (MCRF) approach (i.e., Markov chain geostatistics). This idea directly eliminates conflict transitions, because only one Markov chain is used for multi-dimensional simulation. After spending much effort (multiple years) to explore in multidimensional Markov chain modeling and in modifying the CMC model, it is natural to think of “using a single Markov chain to do multidimensional simulation conditioned on sample data”, while using two or more 1D Markov chains to build nonlinear models always had problems. I was not the only person who thought of that point. A reviewer who reviewed our manuscript also mentioned this point in his/her comments, as he/she stated that "Somebody ever said we probably should use a single Markov chain to do multidimensional simulation, but nobody knows how to do it". So the really difficult thing was “how” to do it - nobody knew at that time. This "how" was exactly what I solved. I spent a long time to think about it. However, the process of transforming the "single chain" idea to the single-chained-based multi-D Markov chain model and further to the MCRF theory (from initial thought to rational equations and further to workable computer code) and eventually getting it to be recognized for publication was a difficult struggle process. In general, the MCRF idea not only solved the small class underestimation problem of the CMC model, but also provided a potentially very generalized spatial statistical approach (Li 2007), as we recently more clearly described in Li et al. (2015).

References:

Cao, G., Kyriakidis, P.C. 2008. Combining transition probabilities in the prediction and simulation of categorical fields. In: Proceedings of the 8th international symposium on spatial accuracy assessment in natural resources and environmental sciences, June 25-27, 2008, Shanghai, China, pp. 25-32. http://www.spatial-accuracy.org/system/files/GuofengCao2008accuracy.pdf.

Elfeki, A.M. 1996. Stochastic characterization of geological heterogeneity and its impact on groundwater contaminant transport. Ph.D. diss. Delft University of Technology.

Elfeki, A.M., and F.M. Dekking. 2001. A Markov chain model for subsurface characterization: Theory and applications. Math. Geol., 33:569–589.

Li, W. 1999. Two-Dimensional Stochastic Simulation of Spatial Distributions of Soil Layers and Types Using the Coupled Markov Chain Method. Postdoctoral report, Catholic University of Leuven, Leuven, Belgium.

Li, W., Zhang, C, et al. 2004. 2D Markov-chain simulation and prediction of shallow subsurface alluvial soil textural layers. Unpublished manuscript.

Li, W. 2007. Markov chain random fields for estimation of categorical variables. Math. Geol., 39(3): 321-335.

Li, W., Zhang, C., Burt, J.E., Zhu, A.X., Feyen, J. 2004. Two-dimensional Markov chain simulation of soil type spatial distribution. Soil Sci. Soc. Am. J., 68: 1479–1490.

Li, W., Zhang, C., Willig, M.R., Dey, D.K., Wang, G., You, L. 2015. Bayesian Markov chain random field cosimulation for improving land cover classification accuracy with uncertainty assessment. Mathematical Geosciences, 47(2): 123-148. doi: 10.1007/s11004-014-9553-y.

Zhang, C., Li, W. 2008. A comparative study of nonlinear Markov chain models in conditional simulation of categorical variables from regular samples. Stoch. Environ. Res. Risk Assess., 22(2): 217-230.